一、建立邻接关系

建立邻接关系

OSPF（Open Shortest Path First）是一种在自治系统（Autonomous System，AS）内部使用的路由选择协议。它采用链路状态路由算法，能够动态计算最短路径，并支持基于IP的路由

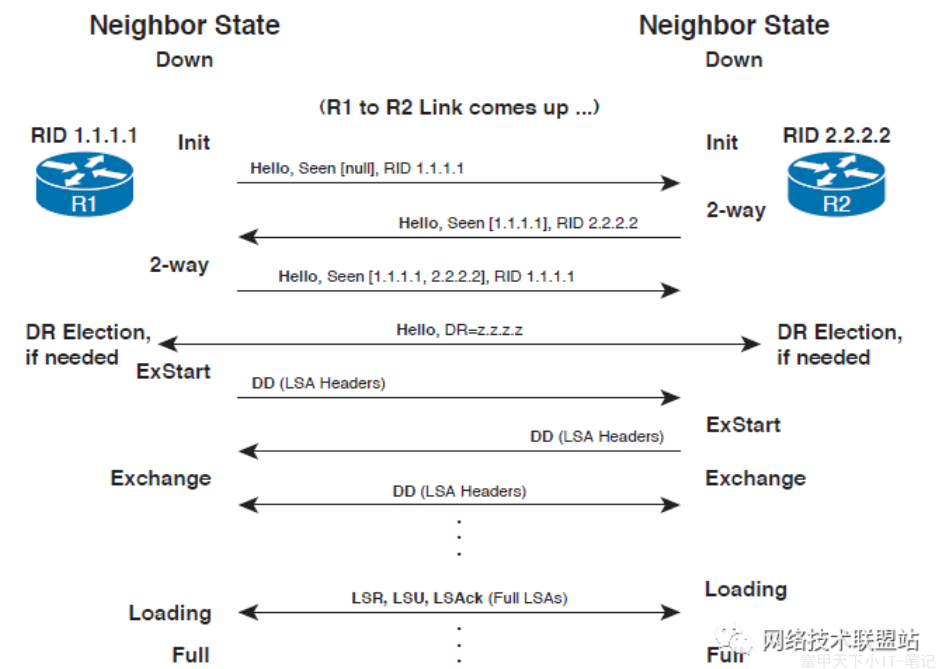
在OSPF中，建立邻接关系是路由器之间进行通信和交换路由信息的前提。下面是建立邻接关系的过程

  1. 本端设备通过接口向外发送Hello报文与对端设备进行通信，用于发现相邻的OSPF路由器

  2. 两端设备进行主/从关系协商，其中一台设备将被选为主设备，负责发送数据库描述报文（Database Description，DD）报文。

  3. 主设备发送DD报文，其中包含了链路状态信息数据库（LSDB）的摘要信息

  4. 从设备收到DD报文后，会检查摘要信息并与自己的LSDB进行比较，确认是否需要更新LSDB

  5. 如果从设备需要更新LSDB，则发送请求更新（Request）报文，请求主设备发送完整的LSDB信息

  6. 主设备收到请求更新报文后，发送Link State Request（LSR）报文，携带具体的LSA（Link-State Advertisement）信息

  7. 从设备收到LSR报文后，发送Link State Update（LSU）报文，携带请求的LSA信息

  8. 主设备收到LSU报文后，更新LSDB，并发送Link State Acknowledgment （LSAck）报文，确认收到LSA信息

  9. 通过上述的DD报文、LSR报文和LSU报文的交换，两端设备完成了链路状态数据库的同步

  10. 当邻接关系建立成功，两端设备可以交换路由信息，为后续的路由计算做准备

下面是一个示例拓扑图，展示了两个OSPF路由器之间建立邻接关系的过程：

示例拓扑图

在上面的拓扑图中，Router1和Router2之间通过Link1和Link2建立了物理连接。这两台路由器通过发送Hello报文进行邻居发现，并使用DD报文进行主/从关系协商和LSA信息交换。最终，两台路由器通过Link3和Link4进行邻居关系建立，并完成链路状态数据库的同步。

二、路由计算

OSPF使用SPF（Shortest Path First）算法进行路由计算，目的是找到到达目标网络的最短路径。以下是OSPF路由计算的过程：

  1. 每个OSPF路由器根据自己的链路状态数据库（LSDB）进行最短路径计算

  2. 首先，每个路由器通过查找自己的LSDB中的链路状态信息，构建一个拓扑图

  3. 在拓扑图中，每个路由器作为一个节点，链路作为边，链路的开销作为边的权重

  4. 路由器根据拓扑图使用SPF算法计算最短路径树，找到到达目标网络的最短路径

  5. SPF算法的计算过程是不断选择权重最小的边，逐步扩展最短路劲树的过程，知道覆盖了所有的节点。

  6. 最终，每个路由器根据最短路径树确定到达目标网络的下一跳路由器和开销

  7. 每当LSDB方发生变化时，路由器会重新计算最短路径，以保证网络的路由收敛性

通过上述的路由计算过程，OSPF能够找到到达目标网络的最短路径，并更新自己的路由表，以便进行数据转发。

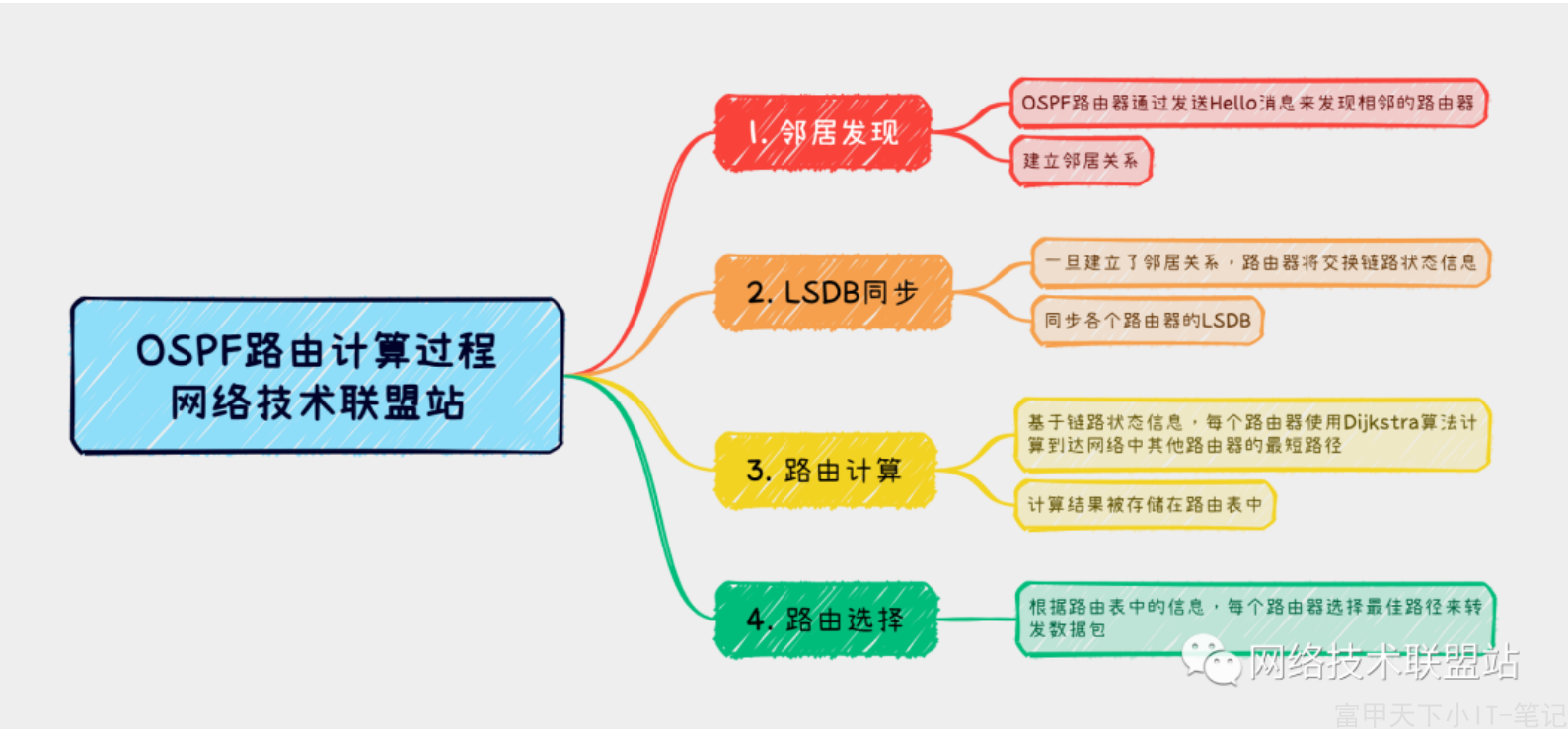
总的来说，OSPF路由计算分文以下几步：

OSPF路由计算步骤

三、OSPF路由计算的算法

OSPF使用Dikstra算法来计算最短路径。Dijkstra算法基于图论，通过迭代计算从一个节点到其他节点的最短路径。

算法步骤如下：

  1. 初始化：将起始节点的距离设置为0，其他节点的距离设置为无穷大。

  1. 选择最短路径节点：从未访问的节点中选择一个距离最短的节点，并将其标记为已访问

  2. 更新邻居节点距离：对于当前节点的所有邻居节点，计算经过当前节点到达邻居节点的距离。如果经过当前节点的距离比邻居节点当前的距离更短，则更新邻居节点的距离。

  3. 重复步骤2和步骤3，知道所有节点都被访问

  4. 根据计算结果生成的路由表。

四、OSPF链路状态数据库（LSDB）

在OSPF网络中，每个路由器维护一个链路状态数据库（LSDB），其中包含了与其他路由器相邻的链路和它们的状态信息。每个链路的状态信息包括链路的带宽、延迟、可靠性等

LSDB

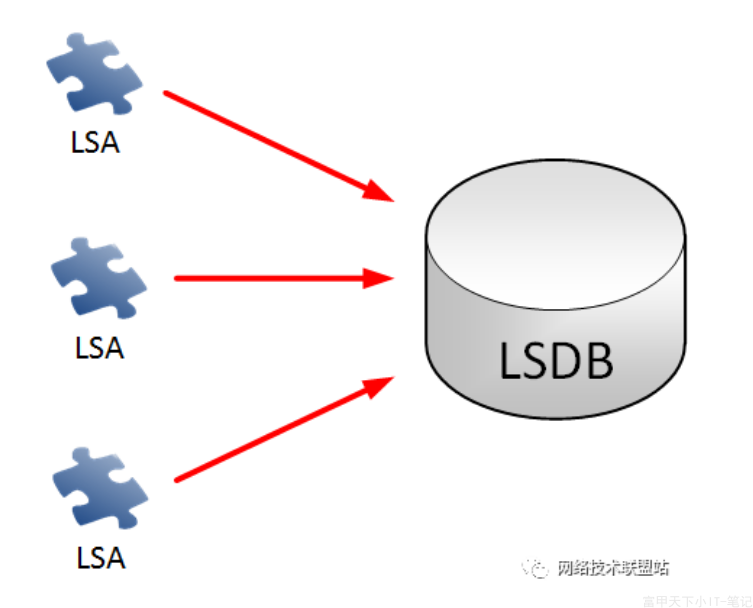
LSDB中的链路状态信息是动态的，路由器会定期交换链路状态更新信息，以保持LSDB的最新状态。

五、生成带权有向图

要生成带权有向图，需要将LSDB中的链路状态信息转化为图的节点和边，并赋予它们适当的权重。下面是生成带权有向图的步骤：

  1. 节点表示：LSDB中的每个路由器被表示为图中的一个节点。节点可以使用路由器的ID或IP地址来标识

    image-20230804143232105

  2. 边表示：LSDB中的每条链路被表示为图中的一条有向边。每个有向边连接两个节点，表示两个路由器之间的连接关系。

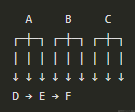
    image-20230804143244397

  3. 边权重：将链路状态信息中的带宽、延迟或其他度量标准作为边的权重。权重反映了连接的质量或代价，可以根据实际情况进行映射。

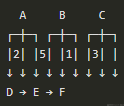
    image-20230804143258392

  4. 图的构建：根据LSDB中的链路状态信息，将每个节点和边添加到图中

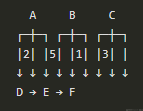
    image-20230804143313860

  5. 有向图表示：使用图的表示方法，如邻接矩阵或邻接表，来表示生成的带权有向图。

六、带权有向图的应用

生成带权有向图后，可以基于该图进行路由计算和路径选择。常用的路由计算算法如Dijkstra算法或最短路径有线（SPF）算法可以应用于该图上，以计算最短路径或优化路径选择。

通过分析带权有向图，可以确定网络拓扑结构中的瓶颈、冗余和性能优化的潜在机会。此外，带权有向图也可用于网络仿真、故障排除和性能分析。